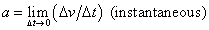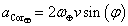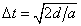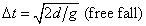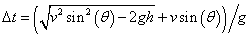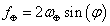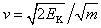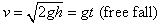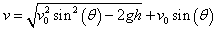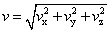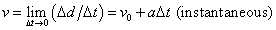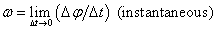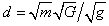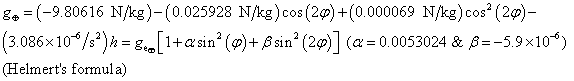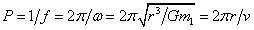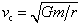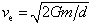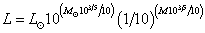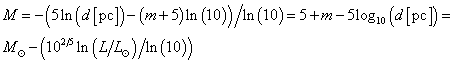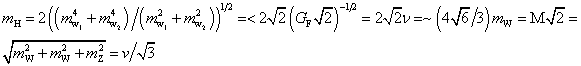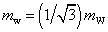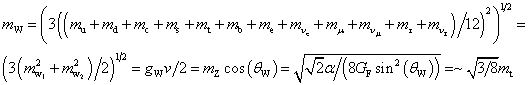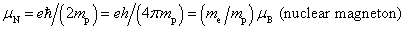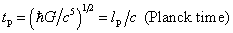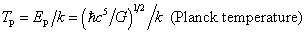Equations
This page is still under construction.
Kinematic Equations
Gravitational Equations
Physical Equations
Wave Equations
Thermodynamic Equations
Electromagnetic Equations
Atomic Equations
Nuclear Equations
Quantum Equations (not finished)
Special Relativistic Equations (not finished)
General Relativistic Equations (not finished)
Cosmological Equations (not finished)
Geometric Equations (not finished)
Mathematical Equations (not finished)
Dimensional Constant Equations (not finished)
Dimensionless Constant Equations (not finished)
Kinematic Equations
a = Δv/Δt = F/m = (vf − vi)/Δt = w/m
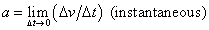
ac = 4π2r/P2 = rω2 = v2/r
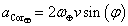
ad = v2/2
aΔt = Δv = vf − vi
a = Δv/Δt = (vf − vi)/Δt
α = a/r = Δω/Δt = T/I (T = torque)
αΔt = ωf − ωi
α = (ωf − ωi)/Δt
d = ½(vi + vf)Δt = (vi + ½aΔt)Δt = viΔt + ½aΔt2 = vΔt
d = ½gΔt2 = vΔt = ((vi + vf)/2)Δt (free fall)
d = W/F
df = di + Δt((vi + vf)/2) = di + vfΔt − ½aΔt2 = di + viΔt + (aΔt2/2) (distance traveled after acceleration; linear equations of motion)
Δφ = larc/r = ωiΔt + ½αΔt2 = ωΔt
Δp = Ft = mvf − mvi = m(vf − vi)
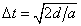
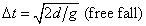
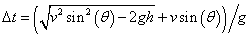
Δt = 2vsin(θ)/g (to hit ground)
Δt = (vf − vi)/a
Δv = vexln(mi/mf) = −vexln(m/(mfuel + m)) (Tsiolkovsky rocket equation)
Δx = v0Δtcos(θ)
Δxtot = (v02/g)sin(2θ)
Δy = v0Δtsin(θ) − ½gΔt2
EK = Iω2/2 = ½mv2 + ½Iω2 = ½mvx2 + ½mvy2 + ½mvz2 = Fd = mad = mv2/2 = wd
f = P−1
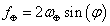
φf = φi + ½(ωi + ωf)Δt = φi + ωfΔt − ½αΔt2 = φi + ωiΔt + ½αΔt2 (angular displacement; rotational equations of motion)
F = ma = m(vf − vi)/Δt
F2 = F12 + F22 − 2F1F2cos(θF1F2)
F1/sin(θF2F3) = F2/sin(θF1F3) = F3/sin(θF1F2)
Fc = −4π2mr/P2 = −mac = −mrω2 = −mv2/r
FCor = maCor
h = vΔtsin(θ) − ½gt2
hmax = v2sin2(θ)/(2g)
j = a/Δt
L = Iω = rp
L2 = m2v2r2
m = F/a = w/g
p = mv = (px2 + py2 + pz2)1/2
P = 1/f = 2π/ω = 2πr/v
P2 = 4π2r/ac
PFoucault = Prot/sin(φ)
t = p2
thmax = vsin(θ)/g
torque = Iα
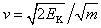
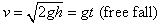
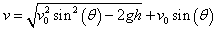
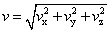
v = 2πr/P = L/(mr) = ωr
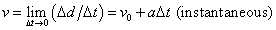
v2 = vx2 + vy2 + vz2
v0y = vsin(θ)
vAB = vA − vB (relative)
vex = I/m
vf = vi + aΔt (final velocity after time Δt)
vf2 = vi2 + 2aΔd (Torricelli's equation; linear equations of motion)
vf − vi = aΔt
vf2 = vi2 + 2ad
vf2 − vi2 = 2ad = 2gd
vf − vi = aΔt
vP = 2πr
v(t) = vexln(m(0)/m(t)) − gt
vx = v0x = v0cos(θ)
vy = v0y − gΔt
v = Δd/Δt = vi + ½aΔt = (vi + (vi + aΔt))/2 = (vi + vf)/2 (average velocity during acceleration)
w = ma = mg
ω = Δφ/Δt = 2πf = 2π/P = v/r
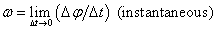
ωf = ωi + αΔt (final angular velocity after time Δt; rotational equations of motion)
ωf − ωi = αΔt
ωf2 = ωi2 + 2αΔφ (rotational equations of motion)
ωf2 − ωi2 = 2αΔφ
ω = ½(ωi + ωf) = Δφ/Δt
yank = mj = F/Δt
W = Fd
z(t) = z0 + v0(t − t0) − ½g(t − t0)2
Gravitational Equations
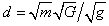
EBG = −Gm1m2/d
EKe = ½mve2 = −EBG = Gm1m2/d
EM = ½mv2 − Gm1m2/r = −Gm1m2/(2r)
EPG = −Gm1m2/d = mgh = −wh
φ = −Gm(3r2 − d2)/(2r3) (inside homogenous sphere)
φ = −Gm/d
FG = −Gm1m2/d2 = −mg = −mv2/r = −w (law of universal gravitation)
FG/FE = −Gm1m2/(Keq1q2)
FT/m2 = (4Gm1dr1)/(d2 − r12)2 ~ 4Gm1r1/d3
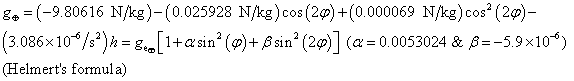
g = FG/m = −Gm/d2 = −v2/r
m = 4π2r3/(GP2)
m = ve2d/(2G) = −gr2/G = −w/g
μ = Gm
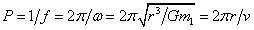
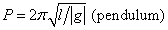
P2 = (4π2/(Gm))r3 = 4π2r/ac
r = (2Gm)1/3P2/3/(2π2/3)
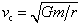
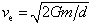
ve2 = 2Gm/d
w = Gm1m2/d2 = ma = −mg
W = EPG2 − EPG1 = Gm1m2((1/d2) − (1/d1))
Physical Equations
d = (M/(2ρNA))1/3 (between ions)
E = EK + EP + EU
EX = EK + EP
I = (2/5)mr2 (sphere)
k0 = ½mv2 + PV + mgh (Bernoulli's equation)
k0 = ½ρv2 + P + ρgh (Bernoulli's equation)
m = MN
m = ρV
M = m/N = NAm
p = (ρ0 − ρ)/ρ0 (ρ0 = pore-free)
P = E/t
P = F/A
Pl = gρh = ρwh
ρ = m/V
tcr = (6 × 108 a) × [(rcluster[Mpc])/(v[Mm/s])]
V = M/(2ρNA) (ion)
V = m/ρ
Wave Equations
d[pc] = 10(1/10)M/510m/5
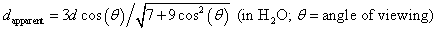
f = f0/[1 + (v/c)cos(θ)]
f = c/λ (EM waves) = v/λ
Φv = ∫(Ev)dA
Iv = Iv0cos2(θ) (transmission of polarized light through polarizer, θ = between light & polarizer)
λ = λ0(1 ± (v/c))
λ = v/f
λn = 2(l/n)
L = LSol10^(MSol103/5/10)(1/10)^(M103/5/10)
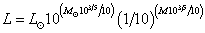
m = (M − 5) + 5log(d/pc)
m = m1 − 2.5log{1 + antilog[−0.4(m2 − m1)]}
M = −(5ln(d/pc) − (m + 5)ln(10))/ln(10) = 5 + m − 5log10(d/pc) = MSol − (102/5ln(L/LSol)/ln(10))
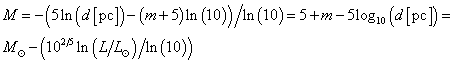
M1 − M2 = 1001/5log(L2/L1)
MSol − M = 1001/5log(L/LSol)
n = c/c0
rE = (2/c)√(Gmdeflectordsourcex(1 − x)) (x = ddeflector/dsource)
Sa = ρva2/V
v = fλ
va = 20.1√(T/°K) = √(1.4P/ρ) = √(1.4RT/m) (gas)
Thermodynamic Equations
ΔEU = ΔH − PΔV
E = (2/3)nEK = kT ≈ Δpγc
Ea = Ei(1 − A) (grey body)
EA = EU − TS
EB = TS
ED = EX + EQ
EG = EV + EA = H − TS
EK = ½mv2 = (3/2)kT
EQ = EA + EB
EY = EX + EA
η = (1/3)ρvrmsλ
φ = λ−1
Φe = 4πr2σT4 = eσT4A
Φe = ∫(Ee)dA
H = EU + PV
He = Eet
κ = λ/(cρ)
K = (log10(P/W) − 6)/10
λ = 1/(π√(2)ρnd2) (d = of mol.) = kη/(ρvrms) (k = 1/3−½) = kT/(π√(2)Pd2)
λ = π2k2γT/(3e2)
λmax = b/T
log(L/LSol) = 3.3log(m/mSol)
L = LSolm3(m/mSol)0.3/mSol3
m = mSol(L/LSol)10/33
M = ρRT/P (ideal gas law)
Me = σT4
Me/λ = c1λ−5e−c2/(λT) = c1λ−5/(ehc/(λkT) − 1)
nv/n = (4/√(π))(m/(2kT))3/2v2e−mv2/(2kT) (nv = n having speed v)
nv/n = (8πm3/h3)(v2/(e(mv2/2) − Emax + 1)) (Fermi distribution)
N = PV/(RT) (ideal gas law)
NRT = (P + (N2a/V2))(V − Nb) (van der Waals equation)
P = (2/3)(n/V)EK = F/A = (n/3)(mvrms2/V) = (NRT/(V − Nb)) − (N2a/V2) (van der Waals equation) = (NR/V)T (ideal gas law) = ρnkT
Pideal = P + (N2a/V2)
P1V1/T1 = P2V2/T2 (ΔN = 0) (combined gas law)
PM = ρRT (ideal gas law)
PV = NRT (universal gas equation)
q = cmΔT = CΔT = C(Tf − Ti) = ΔH = ΔEU + PΔV = Hf − Hi
ρ = PM/RT (ideal gas law)
ρE = (4/c)σT4
(R/NA)T = (2/3)(½mv2)
S = (5/2) + ln[(2πmukT/h2)3/2kT/P]
τ = (1010 a)(m/mSol)−3
T = b/λmax
T = Me1/4/σ1/4 = √(2)L1/4/(2√(r)(πσ)1/4)
Tλ/γ = (π2/3)(k/e)2
v = √(2kT/m)
vrms = √(3kT/m)
vrms2 = 3kT/m
v = √(8kT/(πm))
Videal = V − Nb
V = NRT/P (ideal gas law)
Electromagnetic Equations
a = qE/m = qV/(dm) (of q between 2 V's separated by d)
a = (q/m)(Bv)
a = (q/m)γ−1[E + vB − (v/c)(vE/c)]
B = μ0I/(2πd) (straight wire)
B = μ0nI/(2r) (center of circular coil of n turns)
B = FB/(qvsin(θ)) = μ0H + J = μ0(H − M) = μH = Φ/A = √(Bx2 + By2 + Bz2) = √(2Bxy2 + Bz2)
B = X−1
Bz = Bxytan(φ)
χe = εr − 1
χm = μr − 1 = M/H
C = 4πεr (sphere)
C = q/V
D = εE
ε = D/E = ε0εr
εr = ε/ε0
E = ½CV2 = ½(q2/C) = ½Vq (E stored in capacitor)
E = ½LI2 = ∫(EI)dt (E of I stored in B)
E = D/ε = FE/q = q/(4πε0r2) = σ/ε
EK = mv2/2 = (qBr)2/(2m) = qV
EPE = ½CV2 = ½q2/C = ½qV (capacitor)
EPE = Keq1q2/r = mv2 = qV
ET = I2Rt
f = Bq/(2πm)
F = g(B − Ev)
FB = Bqv = Bqvsin(θBv) = Gg/(4πμd2) = mv2/r
FE = Eq = Keq1q2/r2 = mv2/r = q1q2/(4πεd2) = qVB
FEM = q(E + Bv)
Φ = BA = LI
Φe = (1/(4πε0))(2/3)q2a2/c3
Φe = IV = IR2 (E dissipated by I)
ΦE = q/ε0
γ = 3e2λ/(π2k2T) = J/E = ρ−1
G = 1/R
H = B/μ
I = q/t = V/R
I = qv/(2πr) (I loop)
J = B − μ0H
Λ = R−1
mEM = (2/3)μ(q2/r)
mv = qrB (q in B)
μ = B/H
μ = IA = qL/(2m) = qvr/2 (I loop)
μ = μ0μr
μr = μ/µ0
M = (B/μ0) − H
Me = (1/(4πε0))(q2/(4πc3))(a/r)2sin2(θ)
p = Bqr
p = qr
P = 2πm/(Bq)
P = D – (ε0E)
P/2 = πm/(Bq) = πr/v (q in B)
q = CV (capacitor)
q = ΔΦ/R
q = It
r = mv/(Bq) (q in B)
ρ = Rσ/l (wire)
ρE = ½εE2
ρE = ½μH2
R = Fm/Φ
R = V/I
V = (1/(4πε0))(q/r) = EPE/q = IR = K(q/r)
Y = G + Bi
Y2 = G2 + B2
Ψ = DA
Z = R + Xi
Z = E/H = √(μ/ε) = V/I
abs(Z) = √(R2 + X2)
Atomic Equations
(1/nf2) − (1/ni2) = (ni2 − nf2)/(ni2nf2)
C = nλ = nh/p
ΔE = gμBB (between +½ & −½ in B)
E = −μB (E of interaction with B)
Ei = eVi
EiK = RH(Z − 1)2
EK = ½mv2 = Ze2/((4πε0)2r)
En = −½(Keq1q2/r) = ½mv2 + −(Keq1q2/r) = ½mvn2 = ½(pn2/m) = −2π2K2mq4/(n2h2) = −(m/(2h2))(Ze2/(4πε0))2(1/n2) = −me4/(8h2ε02n2) = −RH/n2 = −RH(Z2/n2)
EPE = −e2/(4πε0r) = Keq1q2/r = m(n2h2/(4π2r2m2)) = −(Ze2/((4πε0)r))
ER = abs(ΔE) = Ei − Ef = EXi − EXf = (h2/(8mL2))(ni2 − nf2) = hf = RH((1/nf2) − (1/ni2))
EX = −(2π2mZ2e4/((4πε0)2h2))(1/n2) = −(Ze2/((4πε0)2r)) = (Ze2/((4πε0)2r)) + [−(Ze2/((4πε0)r))] = −(Zeq/((4πε0)2r))
f = (1/(2π))[e2/((4πε0)mr3)]1/2 = (1/(2π))(v/r) = me4/(4ε02h3n3) = ω/(2π)
f = (2π2mZ2e4/((4πε0)2h3))((1/nf2) − (1/ni2)) = cR((1/nf2) − (1/ni2)) = (Ei − Ef)/h = (me4/(8ε02h3))((1/nf2) − (1/ni2)) = (RH/h)((1/nf2) − (1/ni2))
f = 4π2mZ2e4/(n3h3(4πε0)2)
Fc = mv2/r = Ze2/((4πε0)r²)
fKα = cR∞(Z − 1)2((1/12) − (1/22))
fL = μBB/h = qB/(4πm)
γ = e/(2m)
K = 2π/λ
L = ½(h/(2π)) (intrinsic)
L = mlh = mvr = nh/(2π) = hr/λ
L2 = m2v2r2 = n2h2 = (1/(4πε0))(Ze2/r2)mr
λ = 2μZeq2/(h2α)
λ−1 = R∞((1/nf2) − (1/ni2))
m = MN
μ = −γμBL/h = IA = mlqh/(4πm) = lμB = −μBL/h = −qL/(2m) = qvr/2
p = mlh/(2π)
pn = h/λn
r = (4πε0)h2n2/(Ze2m) = a0n2 = n2h2(4πε0)/(4π2mZe2) = n2h2/(4π2Kemq2) = nh/(mv2π)
v = (1/(4πε0))(Ze2/(nh)) = fλ = nh/(2πrm) = nh/(mr)
Nuclear Equations
A = A0e−λt = λN
A = Z + N
Ar = m/mu
ΔE = Δmc2
Δm = mp − md − mα
−ΔN = λNΔt
ΔN/Δt = λN
EBN = Δmc2 = [Zmp + Nmn − mA]c2
EBN/nN = [ZmH0 + (A − Z)mn − mA0]c2/A
EKα = Q/(1 + (mα/md)) ≈ ((Ap − 4)/Ap)Q
EKd = (½m)(hf/c)2
ER = Ei − Ef = hf
f = (Ar − A)/A
Fn = ρnvn
λ = −ΔN/(NΔt) = ln(2)/t1/2
m = m0(½)^(t/t1/2) = m0e−λt
mα/md ≈ 4/(Ap − 4)
mαvα = mdvd
μ = g√(s(s + 1))μN
N = N0e−λt
N/N0 = e−λt
q = Ze
Q = ½mαvα2((mα/md) + 1) = (½md(mα2/md2)vα2) + (½mαvα2) = ½mdvd2 + ½mαvα2 = Δmc2 = EKd + EKα = [(mA + mB) − (mC + mD)]c2 = (mp − md − me)c2 = (mp − md − mα)c2
r = 3√(A)c (c = 1.2 fm)
ρq(r) = ρq/(1 + e(r − R)/a) (R = (1.07 × 10−15 ± 2 × 10−17)A1/3 m & a = 5.5 × 1014 ± 7 × 1013 m)
σD-D = (288/EK[keV])e−45.8/√(W[keV]) × 10−28 m2
t = −ln(N/N0)/λ
t1/2 = ln(2)/λ = τln(2)
τ = λ−1 = t1/2/ln(2)
vd = (mα/md)vα
X = q[esu]2/(10V[cm3]γ[erg/cm2]) ≈ Z2/(47A)
Quantum Equations
a = (−g/2) − 1 = (abs(μ)/(qsh/m)) − 1
Special Relativistic Equations
a = γ3a0
General Relativistic Equations
a = L/(mc)
a2 + e2 < (Gm/c2)2
α = 1 − (r0/r) + (e2/r2) = 1 − (r0/r) + (e2/r2) − ((1/3)Λr2) + (r0/R) + ((1/3)ΛR2) − (e2/R2)
A = 4π(2Gm/c2)2 = 4π(r+2 + a2)
Cosmological Equations
Geometric Equations
a = ccos(θac) (right triangle)
a/c = cos(θac) (right triangle)
a/sin(θbc) = b/sin(θac) = c/sin(θab)
A = ½ab (right triangle)
A = ½absin(θab) = ½acsin(θac) = ½bcsin(θbc) = bh/2 = √(s(s − a)(s − b)(s − c)) (Heron's formula) (triangle)
A = ½nr2sin(2π/n) (inscribed polygon of n sides, circle)
A = ½s2 (isosceles triangle)
A = (1/4)nl2cot(180°/n) (polygon of n sides)
A = (1/4)πd2 = πr2 (circle)
A = 2Abase + h(a + b + c) = 3lw + bh (triangular prism)
A = 2(lw + lh + wh) (rectangular prism)
A = 2πrh + 2σ = 2πr(h + r) (right circular cylinder)
A = 2πrh (lateral surface area of a right circular cylinder)
A = 4πr2 = πd2 (sphere)
A = 6l2 (cube)
A = bh (parallelogram)
A = h(a + b)/2 (parallelogram/trapezoid)
A = l2 (square)
A = l2 + 2llside (square pyramid)
A = lh = lw (rectangle)
A = nr2tan(π/n) (circumscribed polygon of n sides, circle)
A = πab (ellipse)
A = πrl (lateral surface area of a right circular cone)
A = π(r1 + r2)(r1 − r2) (annulus)
A = πr2 + ½Clside = πr√(r2 + h2) + σ = πr(r + lside) = πr(r + √(r2 + h2)) (right circular cone)
A = Pa/2 (any regular polygon; a = apothem, the distance from the center of the polygon to the center of one side)
A = (w(2h + 2l)) + 2hl (prism)
Aarc = (θarc/360°)πr2
Mathematical Equations
(ab)m = ambm
aman = am + n
(am)n = amn
am(u) = φ
Dimensional Constant Equations
a0 = 4πε0h2/(mee2) = α/(4πR∞)
a0 = 0.3cH
aP = √(c7/(hG)) (Planck acceleration)
AP = tP−1
ε0 = 1/(μ0c2) (electric constant)
Φ0 = h/(2e)
Φ2 = Μ2/(2Λ) = v2/2 (Higgs field)
ΦP = mPlP2/(tP2IP)
G0 = 2e2/h (conductance quantum)
Gβ = GFcos(θC)
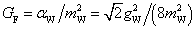
GP = tP3IP2/(mPlP2)
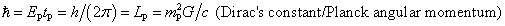
Ke = 1/(4πε0)
KJ = 2e/h (Josephson constant)
Km = μ0/(4π)
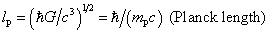
mc2 ≈ mdmt
me1/2 = md1/2 − mu1/2
me1/2 − mμ1/2 = md1/2 − ms1/2
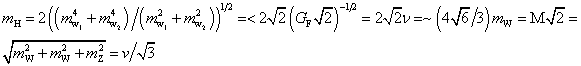
mH2 = 2λν2 = 2Μ2
mμ1/2 − me1/2 = ms1/2 − md1/2
mμ3 ≈ memτ2
mn1/2 − mp1/2 = mΞ−1/2 − mΞ01/2 = mΞc01/2 − mΞc+1/2
mνe1/2 − me1/2 = mu1/2 − md1/2
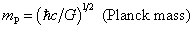
ms² ≈ mumb
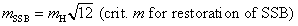
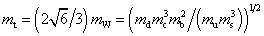
mτ = (mμ3/me)1/2
mtt = mW+ + mW− + mW0
mums3mt2 ≈ mdmc3mb2
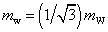
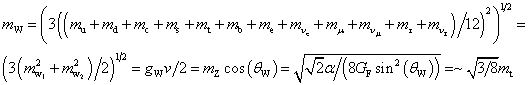
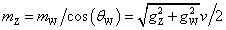
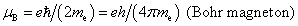
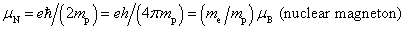
R = NAk
R∞ = α2mec/(2h) = 2pi2mee4/((4πε0)2h3c) = mee4/(8ε02h3c)
RH = R∞hc
RK = h/e2 = μ0c/(2α) (von Klitzing constant)
RP = mPlP2/(tP3IP2)
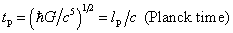
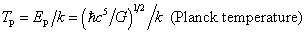

Dimensionless Constant Equations
ae = (abs(μe)/μB) − 1
α = 2πKee2/(hc) = e2/(2ε0hc) = e2/(4πε0hc) = (e/qP)2 = μ0ce2/(2h) (fine structure constant)
αμ < (1.1/2.3) × 10−8 (between μ-ic γ & μ)
αS(E) = 12π/((33 − 2nf)ln(E2/Λ2))
αW = sin2(θW) = 1 − (mW/mZ)2
αW/αS ≈ √(τΔ+/τΣ+)
αW(mZc2) = gW2/(4π)
αX0 = gX02/(4π)